A material is permeable if it contains continuous voids. All materials, such as rocks, concrete, soils, etc., are permeable. The flow of water through all of them obeys approximately the same laws. Hence, the difference between the flow of water through rock or concrete is one of degree. The permeability of soils has a decisive effect on the stability of foundations, seepage loss through embankments of reservoirs, drainage of subgrades, excavation of open cuts in water-bearing sand, rate of flow of water into wells, and many others.
Hydraulic Gradient
When water flows through a saturated soil mass, there is certain resistance to the flow because of the presence of solid matter. However, the laws of fluid mechanics, which apply to the flow of fluids through pipes, are also applicable to the flow of water through soils. As per Bernoulli’s equation, the total head at any point in water under steady flow conditions may be expressed as: Total head = pressure head + velocity head + elevation head
This principle can be understood with regard to the flow of water through a sample of soil of length L and cross-sectional area A, as shown in Fig. 4.1(a). The heads of water at points A and B, as the water flows from A to B, are given as follows (with respect to a datum)


As the water flows from A to B, there is an energy loss, which is represented by the difference in the total heads HA and HB
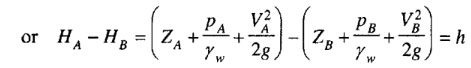
where, PA and PB = pressure heads, VA and VB = velocity, g – acceleration due to gravity, γw = unit weight of water, h = loss of head.
For all practical purposes, the velocity head is a small quantity and may be neglected. The loss of head of h units is effected as the water flows from A to B. The loss of head per unit length of flow may be expressed as i = h/L
Where i is called the hydraulic gradient.
Laminar and Turbulent Flow
Problems relating to the flow of fluids in general may be divided into two main classes:
- Those in which the flow is laminar.
- Those in which the flow is turbulent.
There is a certain velocity, Vc, below which for a given diameter of a straight tube and a given fluid at a particular temperature, the flow will always remain laminar. Likewise, there is a higher velocity, Vt, above which the flow will always be turbulent. The lower bound velocity, Vt of turbulent flow is about 6.5 times the upper bound velocity v of laminar flow as shown in Fig. 4.1(b). The upper bound velocity of laminar flow is called the lower critical velocity. The fundamental laws that determine the state existing for any given case were determined by Reynolds (1883). He found that the lower critical velocity is inversely proportional to the diameter of Soil Permeability and Seepage
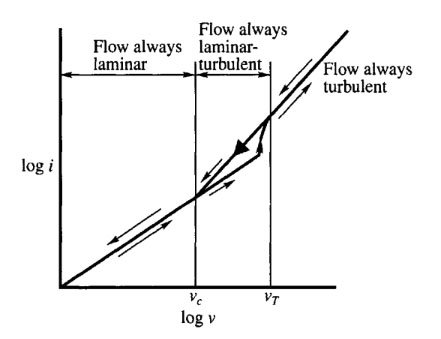
Figure 4.Kb) Relationship between velocity of flow and hydraulic gradient for flow of liquids in a pipe
The pipe gave the following general expression applicable for any fluid and for any system of units.
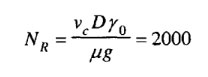
Where, NR = Reynolds Number taken as 2000 as the maximum value for the flow to remain always laminar, D = diameter of pipe, Vc = critical velocity below which the flow always remains laminar, γo = unit weight of fluid at 4 °C, μ= viscosity of fluid, g = acceleration due to gravity.
The principal difference between laminar flow and turbulent flow is that in the former case, the velocity is proportional to the first power of the hydraulic gradient, i, whereas in the latter case it is 4/7 times the power of i. According to Hagen-Poiseuille’s Law, the flow through a capillary tube may be expressed as
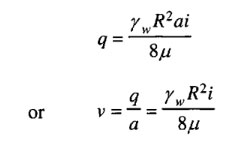
where, R = radius of a capillary tube of sectional area a, q = discharge through the tube, v = average
velocity through the tube, μ = coefficient of viscosity.