Miller Indices:
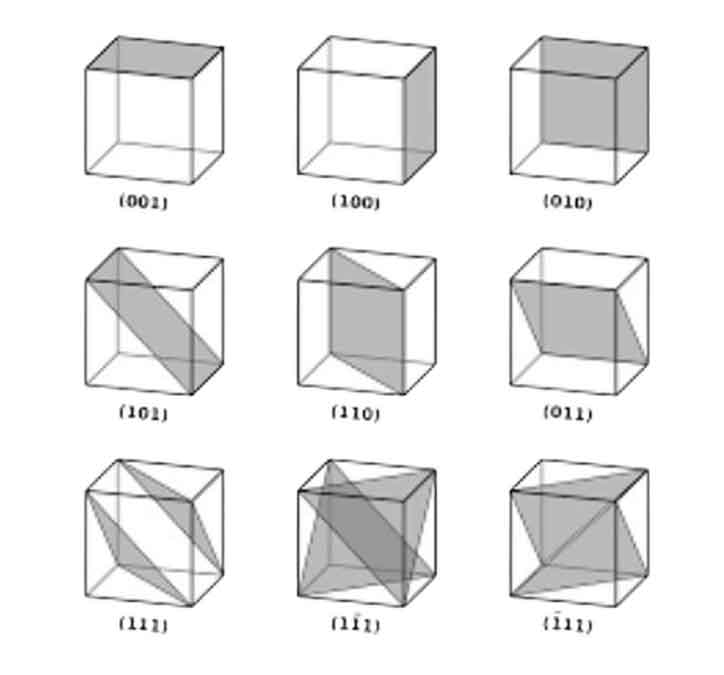
Miller indices for crystallographic planes are the reciprocals of the fractional intercepts (with fractions cleared), which the plane makes with the crystallographic x, y, and z axes of the three nonparallel edges of the unit cell. It consists of a sequence of integers.
Example: (2a, 1/2b, c) = (1⁄2, 2, 1) = (1, 4, 2)
The 4-step procedure of determination of Miller indices:
(1) Find the plane’s intercepts with the x, y, and z axes. If the plane intersects the origin, modify the origin or construct a parallel plane in a different location, such as within an adjacent unit cell.
(2) Take the reciprocal of the intercepts.
(3) Remove fractions.
(4) Enclose in ().
Importance of Miller Indices for crystal directions and planes:
Crystals are usually anisotropic. Their properties differ in different directions. So, it is helpful to regard a crystalline solid as a collection of parallel planes of atoms. So, crystallographers and crystal physicists use a shortened notation to refer to such planes.
The direction of any general vector can also be expressed in terms of a set of indices h, k, l.
Establishing a notation system for atomic planes is crucial as they have a significant impact.
- Optical Properties
- Reactivity
- Surface Tension
- Dislocation
So, the Miller Index is the most helpful way to denote crystal directions and planes.
Determining Miller Indices for Crystal Structures:
Step 1:
Identify the intersection points on the x, y, and z axes. In this case, the intersection point on the x-axis is at x = a, the end (a,0,0), but strictly speaking, the surface is parallel to the y and z axes. Therefore, these two axes do not have an intersection point, but in the particular case where the plane is parallel to the axes, we consider the intersection point to be at infinity (â). So, the intersection points on the x, y, and z axes are
Fractional Intercepts: a, ∞, ∞
Step 2:
To find the intercepts in fractional coordinates, you can convert the coordinates to fractional values by dividing each coordinate by the respective cell dimension. For instance, a point (x,y,z) in a unit cell with dimensions a x b x c will have fractional coordinates of ( x/a, y/b, z/c ). In the case of a cubic unit cell, each coordinate will be divided by the cubic cell constant, a.
Fractional Intercepts: a/a, ∞/a, ∞/a, or simply 1, ∞, ∞.
Step 3:
We must take the fractional intercepts’ reciprocals to obtain the Miller Indices. When specifying a unique surface, these indices should be presented without commas or other symbols and enclosed within standard brackets (….). When dealing with 1 and ∞, their reciprocals are 1 and 0, respectively.
Miller Indices: (100)
Therefore, the surfaces/planes shown are cubic crystal’s (100) faces.
Solution:
- As the plane passes through the current origin, we must choose the new origin at the corner of the adjusted unit cell.
- As related to the new origin, the following intercepts (in terms of lattice parameters a, b, and c) with x, y, and z axes can be referred to: ¥), -1, ½
- The reciprocals of these numbers are 0, -1, and 2, which are already integers.
- Thus, the Miller indices of the considered plane are: (0-12)
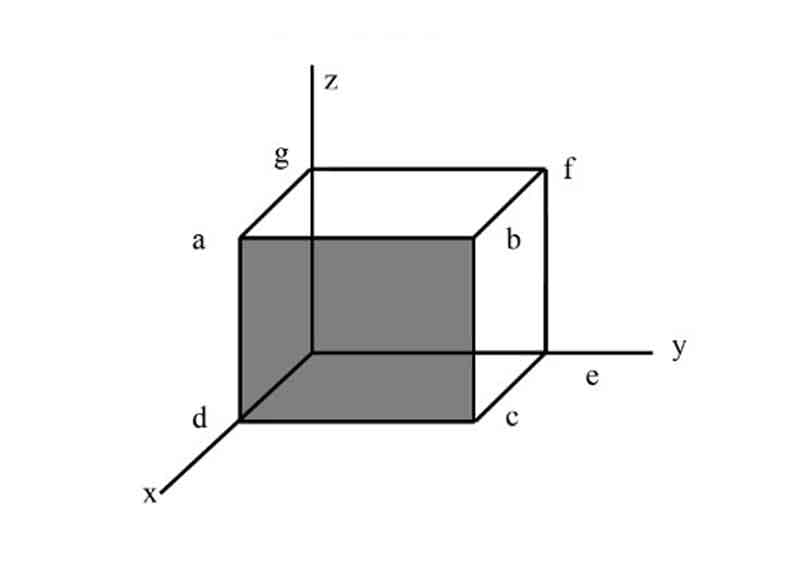
Index system of Miller:
Miller Indices are the series of whole numbers derived from the interrupts or parameters by inverting the whole fraction numbers and clearing the fractions if present.
When a crystal face is parallel to a crystalline axis, it meets the axis at infinity, and the reciprocal
value is 1/∞, which is equal to ‘0’
Here, the abcd face is parallel to the y-axis and z-axis. Thus, the index values that are parallel to these
axes are ‘0’.
Where the crystal face cuts an axis, then the index value is the reciprocal of the intercept.
Here abcd cuts the x-axis at a distance of 1
∴ The index value for the x-axis of the face is represented by 1/1, which equals 1. Here, the reciprocal is unchanged.
But where values are 1/2,1/3,1/4, etc., the indices become 2, 3, 4, etc.