Crystal symmetry refers to the regular arrangement of faces, edges, and other structural features in a crystal. This regularity constitutes the crystal’s symmetry. The degree of symmetry varies in different minerals and is employed in the classification of crystals.
Crystal Symmetry elements:
The geometrical expression of symmetry operation is called crystal symmetry elements. Symmetry elements are the planes, axes, or points around which identical lattice points are symmetrically disposed.
There are three essential elements of symmetry –
- Plane of symmetry or reflection upon a mirror plane.
- Axis of symmetry or reflection about an axis.
- Center of symmetry or reflection through a point.
Another one is the Rotation-Reflection axis.
Plane of symmetry:
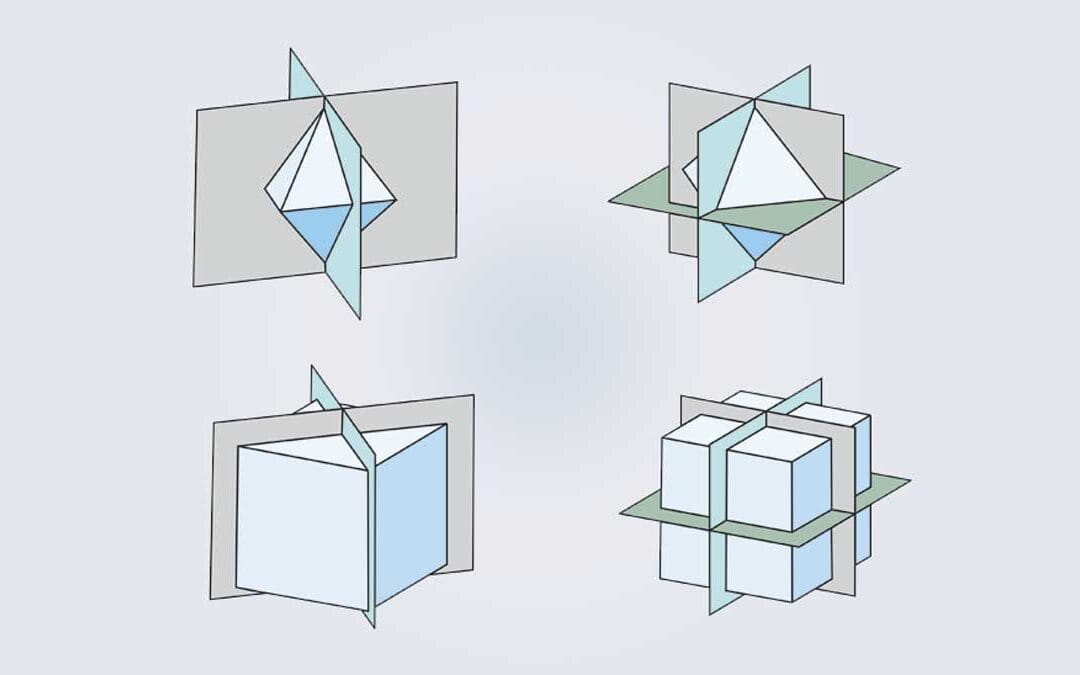
It is an imaginary plane that passes through the center of the crystal and divides it into two parts such that one part is the mirror image of the other. Those planes of symmetry may be diagonal, horizontal, or vertical. It is denoted by P.
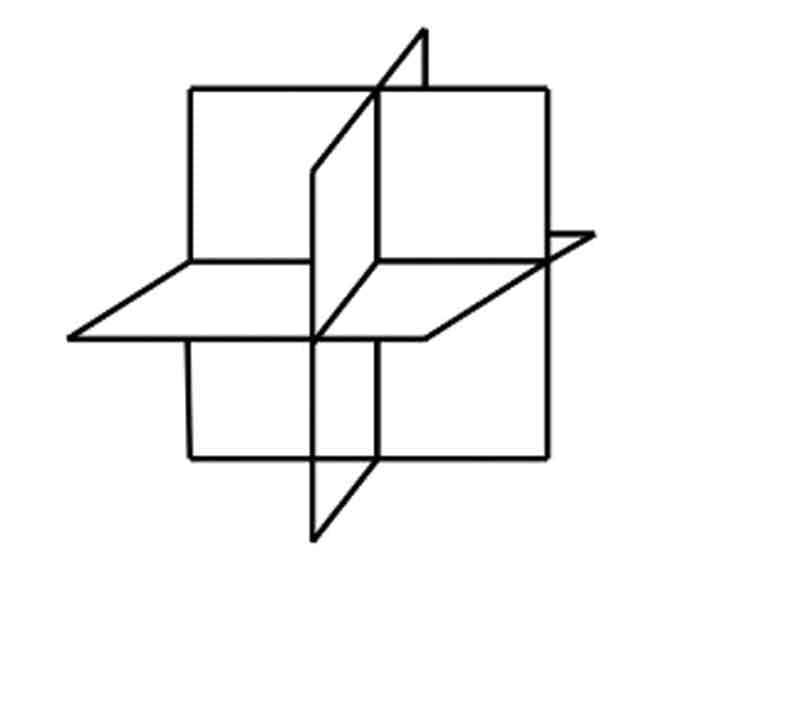
A maximum of nine planes of symmetry are in the normal class of isometric system.
Axis of Crystal symmetry:
The congruent position can be obtained by rotating a figure about a line. The line is called axis of symmetry. The angle of rotation by which a figure is turned into its congruent position is called elementary angle of rotation. The number by which a figure turned into congruent position in a complete rotation is called the fold of an axis.

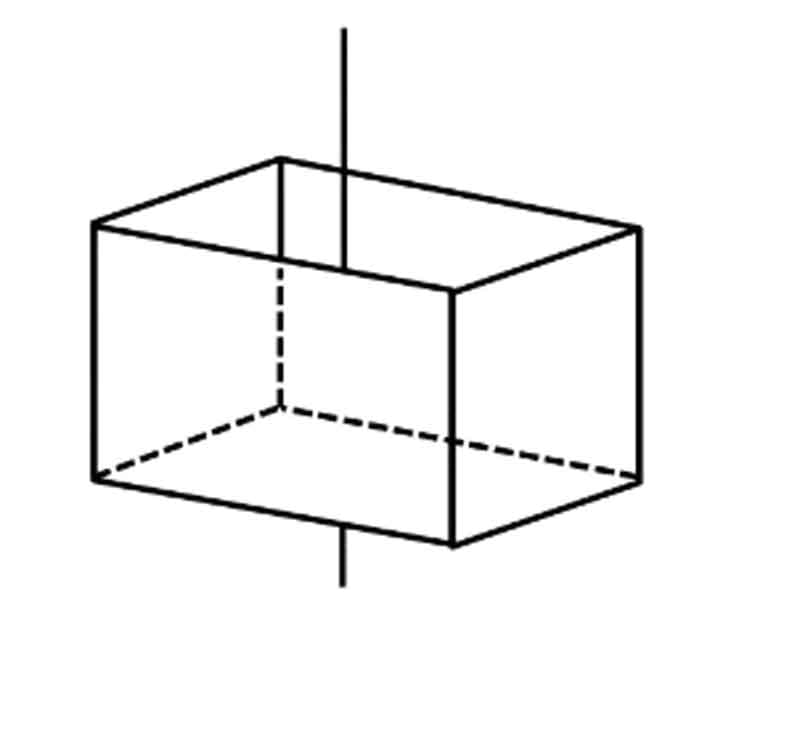
The axis of symmetry is denoted by A. There are 2 fold, 3 fold, 4 fold and 6 fold in a crystal. Maximum number of axis of symmetry is 13, found in normal classes of Isometric System. [3A44A36A2 = 3 + 4 + 6 = 13]
Center of symmetry:
The center of symmetry is similar to the plane of symmetry, but in the case of the plane of symmetry, reflection occurs upon a mirror plane, whereas in the case of the center of symmetry, reflection occurs through a point. If a sample has a center of symmetry, then the same thing can be seen at the same distance through that point in the opposite direction. A crystal has only one center of symmetry. It is also called the center of inverse equality.
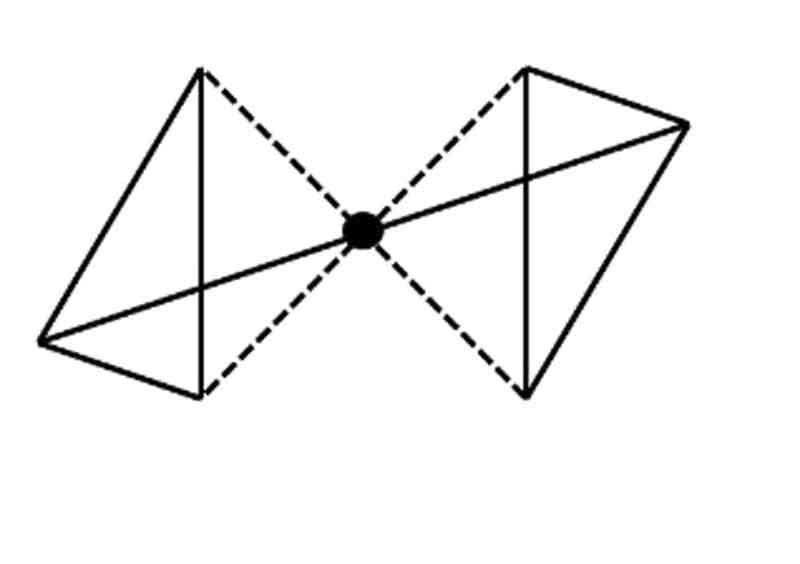
Rotation reflection axis:
This axis is obtained by rotating a figure at a certain angle and reflecting upon a mirror plane perpendicular to the rotation reflection axis. An axis of rotation is an imaginary line through a crystal about which the crystal may be rotated and repeated in its current position 1, 2, 3, 4, or 6 times during a complete rotation.


Combination of Crystal symmetry operations theorem:
Combination symmetry operations are also possible. To create a complete analysis of symmetry about a point in space, we must try all possible combinations of these symmetry operations.
When a figure has two or many symmetry planes (P), the lines of their intersections are symmetry axes (L). The elementary angle of rotation of the respective axis is twice the angle at which the plane intersects.
In the interest of clarity and ease of illustration, we continue to consider 2D examples. Such as:
Reflection across a mirror plane reproduces a motif.
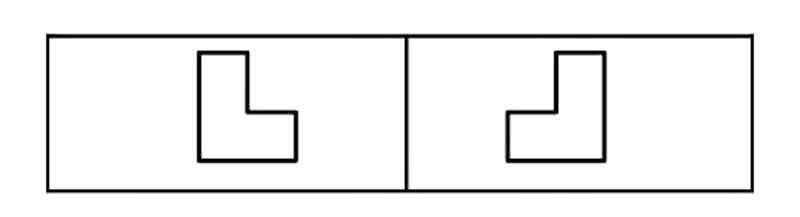
Concept of Symmetry Operations:
Any two figures are mutually symmetrical if they coincide when matched. If a figure has two equal coincident parts, it is auto-symmetrical.
The transformation or matching of two figures of an auto-symmetrical body is called symmetrical operation. The geometrical expression of such a symmetry operation is called an element of symmetry. Symmetry Operations are Reflection through a plane, Rotation, Inversion, Reflection Rotation, and Rotary Inversion.