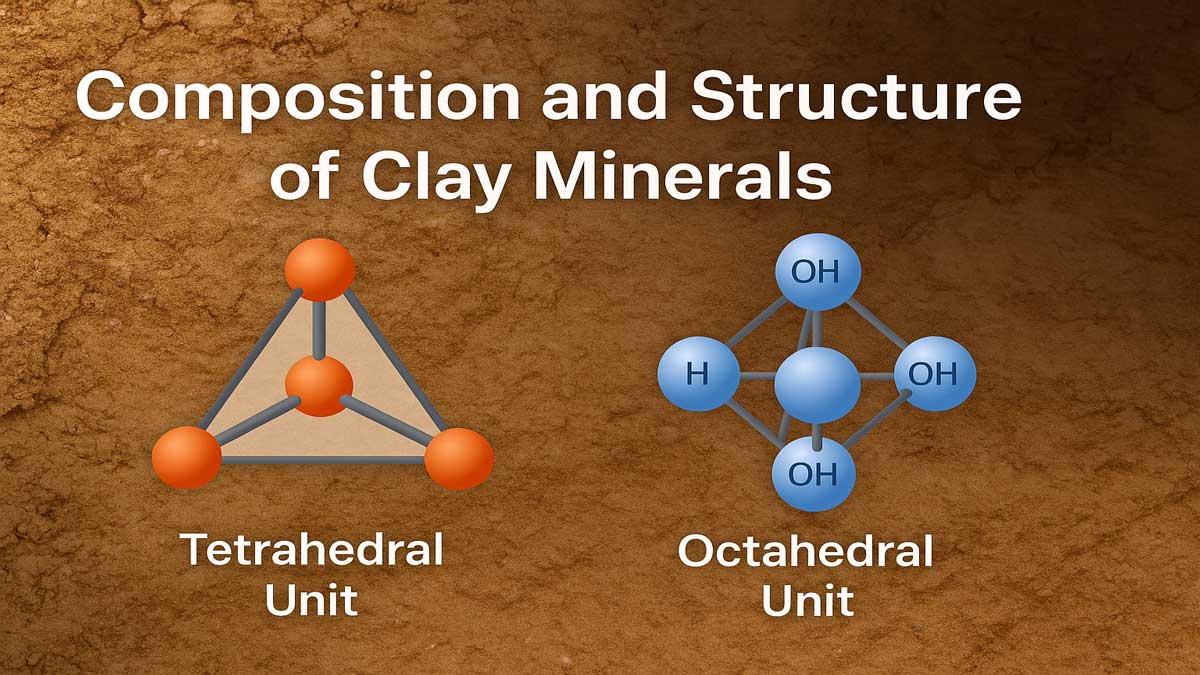
X-ray Crystallography:
X-ray Crystallography is a technique in crystallography in which the pattern produced by X-ray diffraction through the closely spaced lattice of atoms in a crystal is recorded and then analyzed to reveal the nature of that lattice.
Uses:
X-ray crystallography is helpful in:
- Identifying known materials.
- Characterizing new minerals.
- In discerning (recognizing) materials that appear similar to other equipment.
- X-ray crystal structures can account for a mineral’s unusual electronic or elastic properties.
- Shed light on chemical interactions and processes.
- Serve as the basis for understanding enzymatic mechanisms.
- Designing pharmaceuticals against diseases.
Bragg’s Law:
It states, “If we consider an incident beam appear scattering centers at some angle (θ), it can be shown that the only place the scattered beam will be in phase is at the same or ‘reflected’ angle that leaves the scattering points.”
When X-rays strike a crystal layer, some will be reflected. X-rays that add together constructively in X-ray diffraction, analysis of in-phase before and after they are reflected, are done normally.
Constructive interference of the radiation from successive planes occurs when the path difference is an integral number of wavelengths. That is –
nλ = 2dsinθ
This is Bragg law with the Bragg Equation.
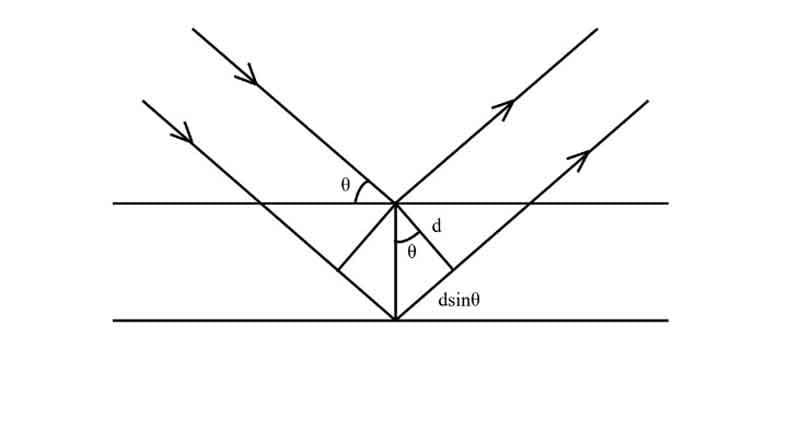
Determination of X-ray scattering using Bragg equation:
Crystals are regular arrays of atoms, and X-rays can be considered waves of electromagnetic radiation. Atoms scatter X-rays as spherical waves, a phenomenon known as scattering. A regular array of scatters produces a regular array of spherical waves.
If we consider an incident beam approaching scattering centers at some angle θ, it can be shown that the place where the scattered beam will be in phase is at the same or ‘reflected’ angle that leaves the scattering points.
In the figure,
a1, a2, a3 = Plane nets or nets of the plane.
1, 2 = Bundle of ray.
If the two planes are to be scatted in phase, then the phase difference Δ must equal an integral number of wavelengths nλ. That is –
Δ = nλ, where n = 1, 2, 3, … … …
The phase difference between rays 1 and 2 in the figure is –
Δ = AC – BC … … … (i)
From ΔABC, we have –
BC/AC= cos 2θ
⇒ BC = ACcos2θ
∴ From (i), we have
Δ = AC – ACcos2θ
= AC (1 – cos2θ)
= 2ACsin2θ
Here, θ = glancing angle.
From ΔADC, CD = d
∴ sinθ = CD/AC
⇒ AC = D/sinθ
∴ Δ = 2. D/sinθ. sin2θ
⇒ nλ = 2dsinθ [as, Δ = nλ].
This is Bragg’s Equation for diffraction.
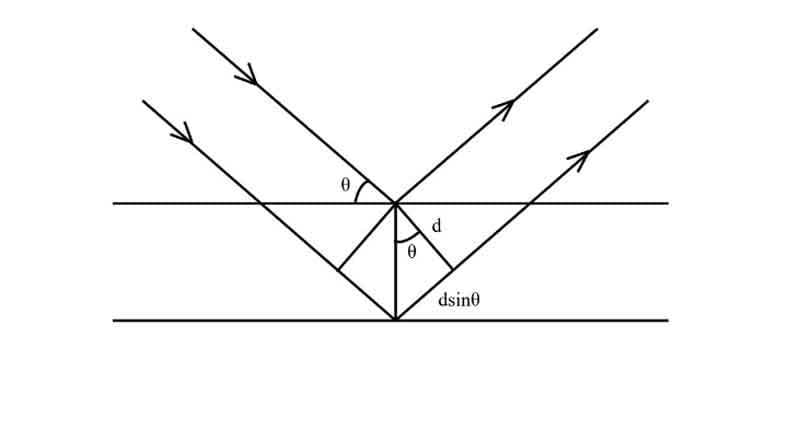
How it enables the determination of d-spacing within mineral structures:
A crystal behaves as a 3D diffraction grating for X-rays. In a diffraction experiment, the spacing of lines on the grating can be deducted from the separation of the diffraction maxima.
Measuring the relative intensities of different orders can provide information about the line structure on the grating.
Similarly, measuring the separation of the X-ray diffraction maxima from a crystal allows us to determine the size of the unit cell. From the intensities of diffracted beams, one can obtain information about the arrangement of atoms within the cell.