A function is a fundamental mathematical concept that establishes a relationship between inputs and outputs. Understanding different types of operations is important because they form the basis of mathematical modeling, calculation, and problem-solving in many scientific disciplines.
What is a Function?
Function:
A function is a relationship between a set of inputs and possible outputs, with the property that each input is associated with exactly one output. Consider A and B as any two non-empty collections. A mapping from A to B is a function if every element in set A has an endpoint and set B has exactly one image.
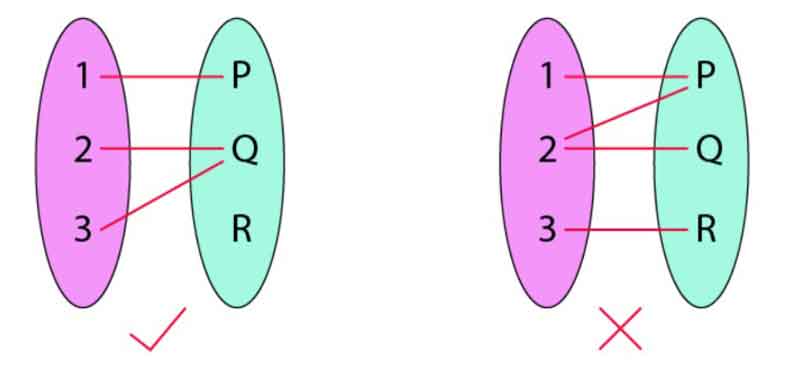
Another definition of a function is that it is a relation “f” such that each element of a set “A” is assigned to exactly one element belonging to a set “B.” A function cannot also contain two pairs with the same first element.
Why is Understanding Types of Functions Important?
Functions are important in mathematics and their practical applications in the real world. Engineers use functions to describe physical systems, and economists use functions to make decisions about money. Scientists use functions to explain natural phenomena. Understanding the types of functions can help you solve different problems.
Types of Functions:
One–one function (Injective function):
If every element in a function’s range possesses a unique image in the target set, the function is referred to as a one-one function.
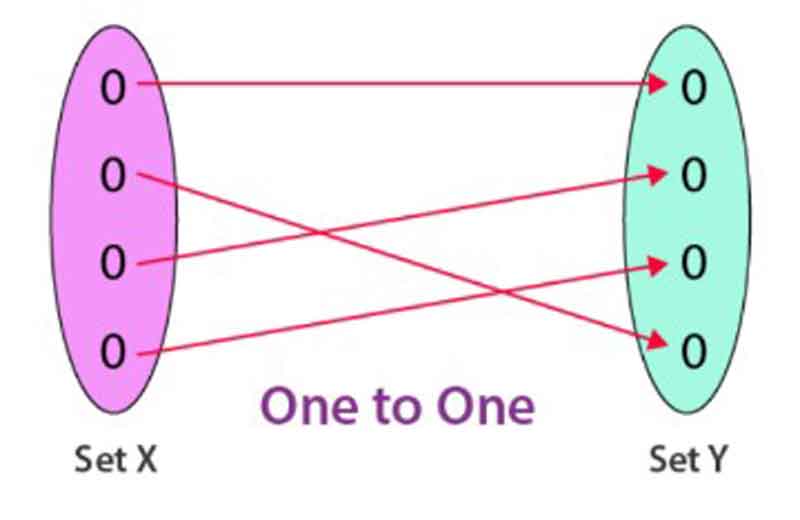
For example, the function f: R → R is defined as f(x) = 3x + 5 and classified as a one-to-one function.
Many – one function:
On the other hand, if two parts of the region are of the same shape, the function is said to be many-to-one.
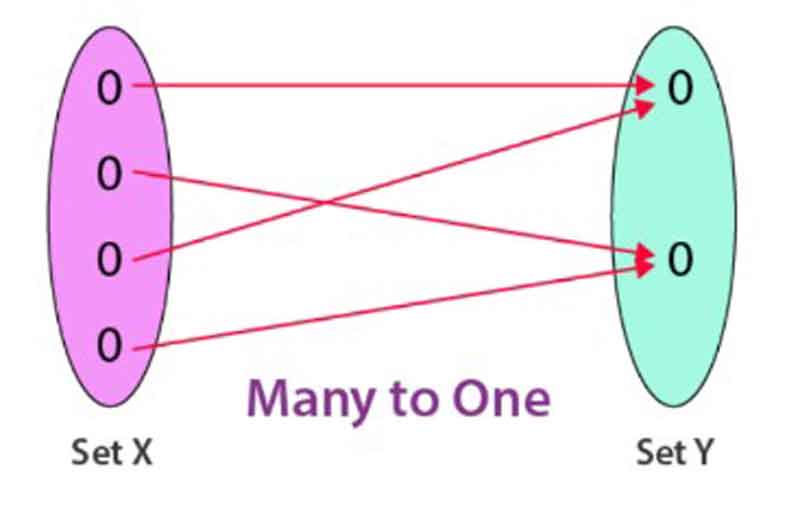
For example, the function f: R → R defined by f(x) = x² + 1 is classified as many-to-one.
Onto–function (Surjective Function):
A function is considered open if each element of the range of values in the specified array has one first character.
Into – function:
If an element in the value range is not the same as an element, the assignment will be converted to an assignment.
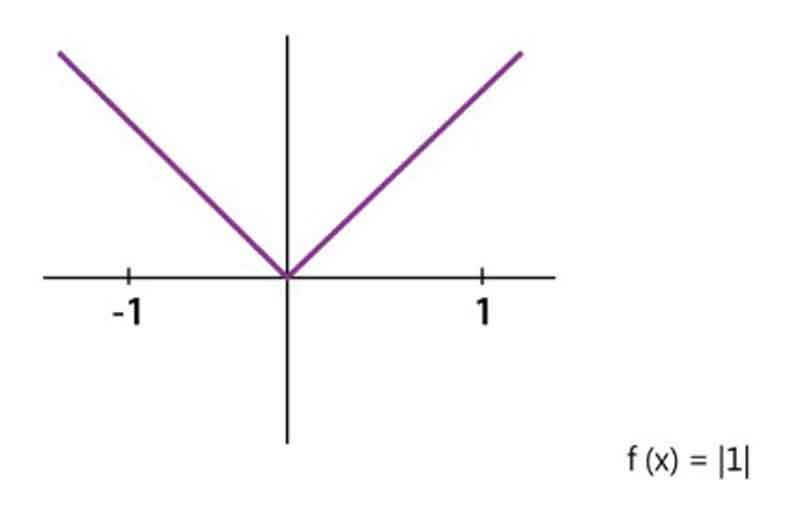
Let A be defined as the set of all x such that 1 is less than x and x is less than 1, equivalent to the set B. Consider the mapping f: A → B and analyze the characteristics of the specified function P. Where F(x) equals the absolute value of x, denoted as |x|.
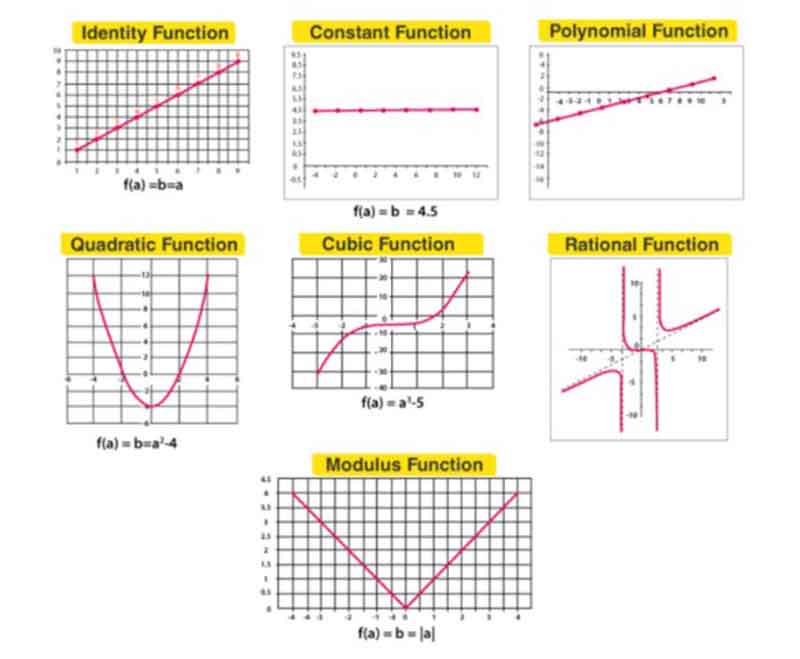
Polynomial function:
The degree of a polynomial function is determined by the most prominent exponent in the expression. Hence, a polynomial function can be expressed as f(x) = anxn + an-1 x n-1 + … + a1x1 + a0. If a polynomial function has a degree of 0, it is called a constant function.
- If the degree is 1, the polynomial function is said to be linear.
- If the degree is 2, then the polynomial function is quadratic.
- If the degree is 3, then the polynomial function is of degree 3.
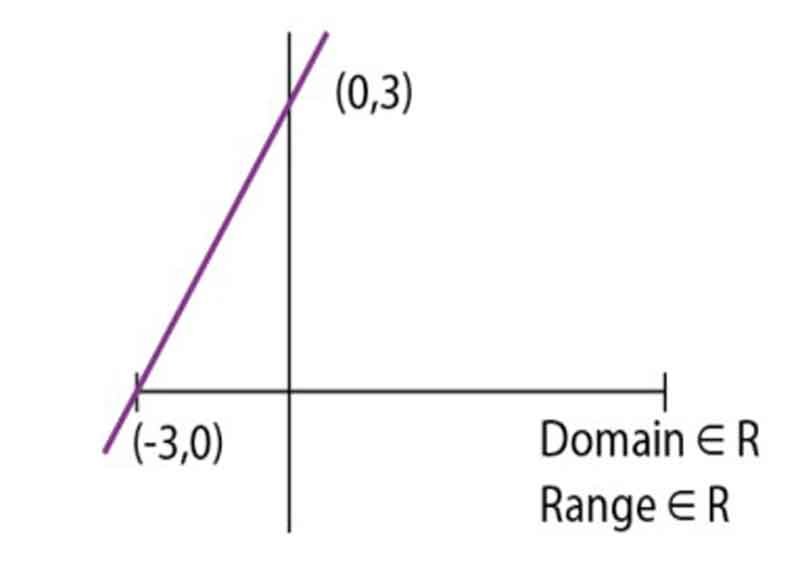
Linear Function:
All functions represented in the format ax + b, where a and b are real numbers, and a is not equal to zero, are classified as linear functions. The corresponding graph will depict a straight line. To put it another way, a linear polynomial function represents a first-degree polynomial in which the variable is multiplied by m, and an additional constant, c, is added. It can be formulated as f(x) = mx + c.
For example, f(x) = y = x + 3
Identical Function:
Two functions, f, and g, are considered identical if.
(a) The domain of f = domain of g
(b) The range of f = the Range of g
(c) f(x) = g(x)A x ∈ Df & Dg
Quadratic Function:
Quadratic functions are defined as all functions that can be expressed in the form y = ax² + bx + c. Where a, b, and c are real numbers, and a is not equal to zero. The graph of such functions will exhibit a parabolic shape.
Rational Function:

Algebraic Functions:
An algebraic equation is defined as a function that comprises a finite number of terms, which include powers and roots of the independent variable x, along with basic operations such as addition, subtraction, multiplication, and division.
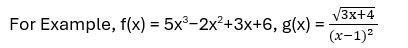
Cubic Function:
A cubic polynomial function is defined as a polynomial of degree three, represented in the form F(x) = ax³ + bx² + cx + d, where the coefficient a is non-zero.
Even Function:
A function f is classified as an even function if it satisfies the condition f(-x) = f(x) for all values within its domain. For example, f(x) = cos(x).
Odd Function:
A function f is classified as an even function if it satisfies the condition f(-x) = -f(x) for all values within its domain. For example, f(x) = sin(x) is an even function.
Periodic Function:
A function is deemed periodic if a positive real number T exists, such that f(u – t) = f(x) for every x in the domain range.
For example f(x) = sinx
The equation f(x + 2π) = sin(x + 2π) = sin(x) establishes that the fundamental period of the sine function, sin(x), is 2π.
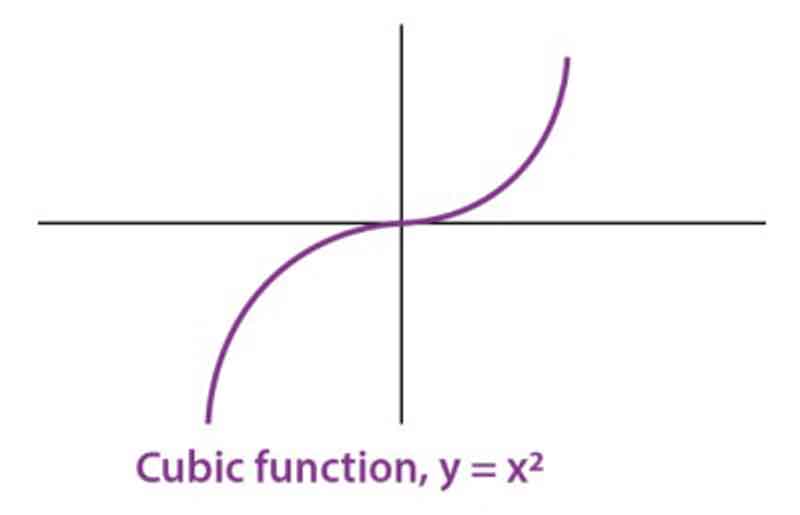
Constant Function:
The function f: P → P is defined by b = f(x) = D, where a is an element of P and D is a constant P element. This indicates that f is a constant function.
• Domain of f = P
• Range of f = {D}
• The graph represents a linear function that runs parallel to the x-axis.
A polynomial of degree zero can be defined as f(x) = f(0) = a_{0} = c. This means that irrespective of the input value, the output remains constant. The graphical representation of such a polynomial is a horizontal line.
Identity Function:
P= set of real numbers
The function f : P → P, characterized by the relation b = f(a) = a for every element belonging to the set P, is called the identity function.
• Domain of f = P
• Range of f = P
• The graph represents a linear function that intersects the origin.
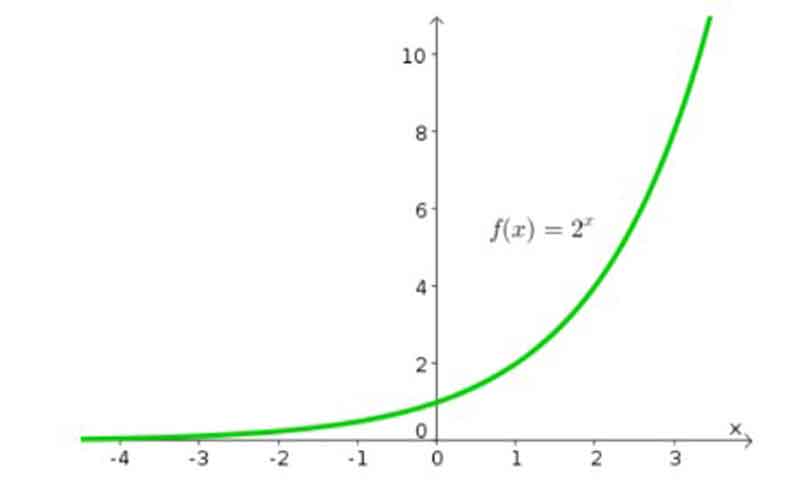
Exponential Function:
The exponential function is regarded as one of the key functions in mathematics. However, it must be acknowledged that the linear function holds even greater significance. The independent variable is designated as the exponent to construct an exponential function. A straightforward illustration of this concept is the function f(x) = 2x.
Logarithmic Functions:
Logarithmic functions serve as the inverses of exponential functions, and every exponential function can be represented in logarithmic form. Likewise, all logarithmic functions can be converted into exponential form. Logarithms are particularly valuable as they allow for the computation of large numbers while facilitating operations with significantly smaller, more manageable figures.
Conclusion:
Understanding different types of functions is essential to address mathematical problems and their applications in science, technology, and engineering. Each category is useful in different geographical areas, with various properties, applications, and customized manufacturing capabilities.